Text
Unit E4 Section 3
Standard Deviation

The two frequency polygons drawn on the graph below show samples which have the same mean, but the data in one are much more spread out than in the other.

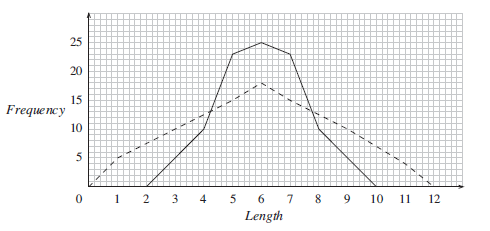
The range (highest value – lowest value) gives a simple measure of how much the data are spread out.

Standard deviation (s.d.) is a much more useful measure and is given by the formula:

Then (xi − x)2 gives the square of the difference between each value and the mean (squaring exaggerates the effect of data points far from the mean and gets rid of negative values), and

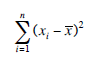
sums up all these squared differences.

The expression

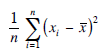
gives an average value to these differences. If all the data were the same, then each xi would equal x and the expression would be zero.

Finally we take the square root of the expression so that the dimensions of the standard deviation are the same as those of the data.

So standard deviation is a measure of the spread of the data. The greater its value, the more spread out the data are. This is illustrated by the two frequency polygons shown above. Although both sets of data have the same mean, the data represented by the 'dotted' frequency polygon will have a greater standard deviation than the other.

Worked Examples

1

Find the mean and standard deviation of the numbers,

6,   7,   8,   5,   9

The mean, x, is given by,

x =
=
= 7

Now the standard deviation can be calculated.

s.d. =
=
=
=
= 1.414 (to 3 decimal places)

An alternative formula for standard deviation is

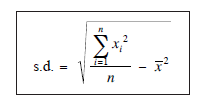
This expression is much more convenient for calculations done without a calculator. The proof of the equivalence of this formula is given below although it is beyond the scope of the GCSE syllabus.

Proof

You can see the proof of the equivalence of the two formulae by noting that

2

Find the mean and standard deviation of each of the following sets of numbers.

(a)

10,   11,   12,   13,   14

The mean, x, is given by

x =
=
= 12

The standard deviation can now be calculated using the alternative formula.

s.d. = ⎛
⎝⎞
⎠ − 122
=
=
= 1.414 (to 3 decimal places)
(b)

5,   6,   12,   18,   19

The mean, x, is given by

x =
= 12 (as in part (a))

The standard deviation is given by

s.d. = ⎛
⎝⎞
⎠ − 122
=
= 5.831 (to 3 decimal places).

Note that both sets of numbers have the same mean value, but that set (b) has a much larger standard deviation. This is expected, as the spread in set (b) is clearly far more than in set (a).
3

The table below gives the number of road traffic accidents per day in a small town.

Find the mean and standard deviation of this data.

The necessary calculations for each datapoint, xi, are set out below.

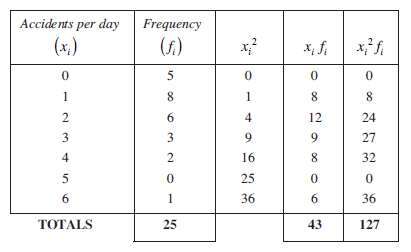
From the totals,

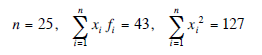
The mean, x, is now given by

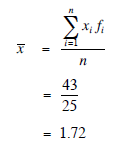
The standard deviation is now given by

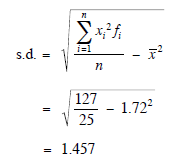
Most scientific calculators have statistical functions which will calculate the mean and standard deviation of a set of data.

Exercises

On this page round your results to 2 decimal places if necessary.

Find the mean and standard deviation of each set of data given below.

MeanStandard Deviation
A
B
C

Two machines, A and B, fill empty packets with soap powder. A sample of packets was taken from each machine and the weight of powder (in kg) was recorded.

(a)

Find the mean and standard deviation for each machine.

Machine A

mean: kg

standard deviation:

Machine B

mean: kg

standard deviation:

(b)

Which machine is most consistent?

On average, the boxes filled by weigh less than the boxes filled by , but is more accurate.

When two dice were thrown 50 times the total scores shown below were obtained.

Find the mean and standard deviation of these scores.

mean:

standard deviation:

The length of telephone calls from an office was recorded. The results are given in the table below.

Estimate the mean and standard deviation using this table.

mean:

standard deviation:

Thirty families were selected at random in two different countries. They were asked how many children there were in each family.

Find the mean and standard deviation for each country and comment on the results.

Estimated
Mean		Estimated
Standard Deviation
A
B
On average, the sizes of the families in are smaller and less spread out than in .

Ten students sat a test in Mathematics, marked out of 50. The results are shown below for each student.

25,   27,   35,   4,   49,   10,   12,   45,   45,   48

(a)

Calculate the mean and standard deviation of the data.

mean:

standard deviation:

The same students also sat an English test, marked out of 50. The mean and standard deviation are given by

mean = 30, standard deviation = 3.6.
(b)

Comment on and contrast the results in Mathematics and English.

The means in both Mathematics and English are identical, but the marks in are less spread out than in .

There are twenty students in class A and twenty students in class B. All the students in class A were given an I.Q. test. Their scores on the test are given below.

100,   104,   106,   107,   109,   110,   113,   114,   116,   117,
118,   119,   119,   121,   124,   125,   127,   127,   130,   134.

(a)

The mean of their scores is 117. Calculate the standard deviation.

(b)

Class B takes the same I.Q. test. They obtain a mean of 110 and a standard deviation of 21. Compare the data for class A and class B.

has, on average, higher and less spread out I.Q. scores than .
(c)

Class C has only 5 students. When they take the I.Q. test they all score 105. What is the value of the standard deviation for class C?

In a survey on examination qualifications, 50 people were asked,

"How many subjects are listed on your GCSE certificate?"

The frequency distribution of their responses is recorded in the table below.

(a)

Calculate the mean and standard deviation of the distribution.

mean:

standard deviation:

(b)

A Normal Distribution has approximately 68% of its data values within one standard deviation of the mean.

Use your answers to part (a) to check if the given distribution satisfies this property of a Normal Distribution.