Equations of the form
are called quadratic equations. Many can be solved using factorisation. If a quadratic equation can be written as
(x − a)(x − b) = 0
then the equation will be satisfied if either bracket is equal to zero. That is,
(x − a) = 0 or (x − b) = 0
So there would be two possible solutions, x = a and x = b .
Worked Examples
Solve x2 + 6x + 5 = 0 .

Factorising gives
(x + 5)(x + 1) = 0
So
x + 5 = 0 or x + 1 = 0
therefore
x = −5 or x = −1
Solve x2 + 5x − 14 = 0.

Factorising gives
(x − 2)(x + 7) = 0
So
x − 2 = 0 or x + 7 = 0
therefore
x = 2 or x = −7
Solve x2 − 12x = 0.

Factorising gives
x(x − 12) = 0
So
x = 0 or x − 12 = 0
therefore
x = 0 or x = 12
Solve
4x2 − 81 = 0

Factorising gives
(2x − 9)(2x + 9) = 0
So
2x − 9 = 0 or 2x + 9 = 0
therefore
| x | = or x | = |
| = | = |
Solve x2 − 4x + 4 = 0.

Factorising gives
(x − 2)(x − 2) = 0
So
x − 2 = 0 or x − 2 = 0
therefore
x = 2 or x = 2
This type of solution is often called a repeated solution and results from solving a perfect square, that is
(x − 2)2 = 0
Most of these examples have had two solutions, but the last example had only one solution.
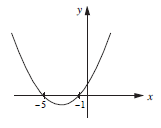
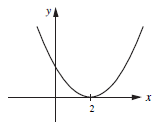
The graphs below show
| y = x2 + 6x + 5 | and | y = x2 − 4x + 4. |
|
The curve crosses the x-axis at x = −5 and x = −1. These are the solutions of x2 + 6x + 5 = 0 |
The curve touches the x-axis at x = 2 This is the solution of x2 − 4x + 4 = 0 |