From the Exploring Data website - http://curriculum.qed.qld.gov.au/kla/eda/
© Education Queensland, 1997

Sex Partner Puzzle

The results of a sex survey conducted in the Chicago area had results that claimed the average number of sex partners was 6 for men and 2 for women.

Let’s make these simplifying assumptions (all of which are reasonable):

Is it possible that the men's average could be 6 and the women's 2? If you believe it is possible, devise an example. If you believe it isn’t possible, prove that it is not possible.

The sex survey is real. This topic generated a large amount of interesting traffic on the alt.rec.puzzles newsgroup. Here is some of the discussion from the newsgroup.

**

Suspicious indeed!

If they were counting only male-female relations, and if males and females agreed on what constituted a sexual partnership, and there were equal numbers of males and females, then the average should be exactly the same. Imagine a graph made of two columns of nodes, one for males, and one for females. A relationship between a particular male and female would be represented as an arc joining the corresponding female and male nodes. The average number of relationships for males would be the total number of arcs divided by the number of males. For females it would be the number of arcs divided by the number of females.

If there were more females than males (as I think there are), the female average would be lower, but only in (inverse) proportion to their relative numbers, i.e. only a few percent, way below the resolution of the reported results.

Of course, males and females may not agree on what constitutes a sex partnership. If this were the whole explanation, males seem to be three times as likely to designate a situation a partnership as females.

Or, same-sex partnerships may be counted in the statistics. If that were the whole explanation, and since each male-male pairing counts as two for males and zero for females, it would imply that males, on average have at least as many homosexual encounters as heterosexual ones. This could be achieved by a small subset of males if they had far more than the average number of encounters. Eg, if the burden had to be carried by 10% of the males, each of that 10% would have to average about 20 sex partnerships with other males.

Or, of course, the respondents could just be lying.

*****

Yes, if by "average" you mean arithmetic mean, then I think you are right. The average is equal to the total number of all sex partnerships divided by N, for both men and women.

Currently in the UK, school children are taught is statistics classes that there are three kinds of average - the mean, the median and the mode (presumably geometric mean is too hard). Maybe your survey is referring to the mode - i.e. most common value, rather than the mean. Then the figures can be explained by relatively few women having a very large number of partners.

***

The men lie by exaggerating their number of sexual partners, and the women lie by underreporting theirs.

***

As a survey of course, there could be a sampling error. However, I tend to think either someone's lying, or this is sheep country.

***

The Answer

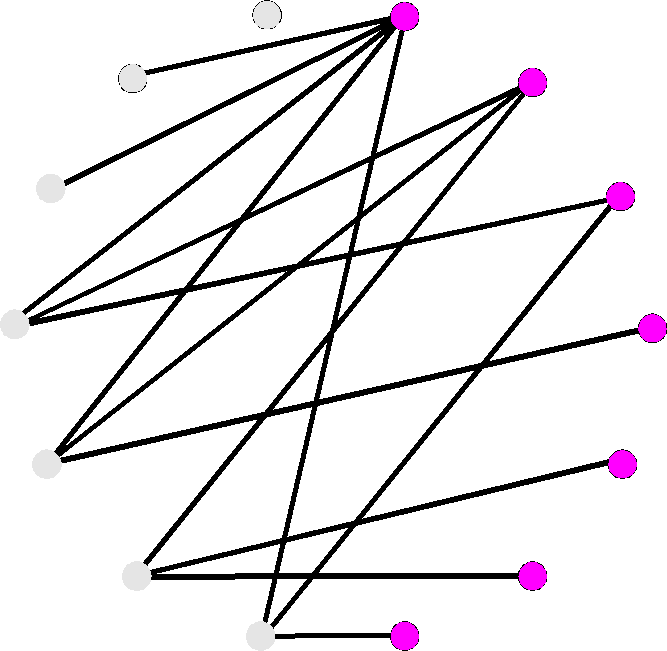It isn’t possible if you take the average to be the mean, for the reason given in the first post to alt.rec.puzzles. But if you use the median it is quite possible. One respondent said, ‘This fits with data I've heard from other surveys, that there are a very few women who go round sleeping with all the men, skewing the statistics in precisely this way.’

The diagram gives an example with seven men and seven women. Each light grey dot represents a man and each pink dot represents a women. A line connecting two dots indicates that they were sex partners. The men have fourteen liaisons in total, for a mean of two. Obviously the women must have the same number of liaisons (since every line has two ends) so the women's mean is also two. But the median is a different story. Sorting the men's data gives us 0 1 1 3 3 3 3 for a median of 3 partners. After the women's data is sorted we have 1 1 1 1 2 3 5 for a median of 1 partner. The medians do not necessarily have to be equal.

And of course there may have been a little bit of bragging.

The next section is the Sanitised Version of the Sex Partner Puzzle, possibly more suitable for high school students.

How Many People Have You Dated?

An anonymous survey was conducted in a Brisbane high school asking the seniors how many other seniors in that school they had dated or were currently dating. The same number of male and female students responded. The average response by the males was 3 females, while the average response by the females was 1 male.

The question is, is it possible for the boy’s average to be 3 while the girl’s average is only 1? When giving your answer, clearly state any assumptions you have made. If it not possible, show why it isn’t possible. If it is possible, give an example of how this can occur.

Solution

It isn’t possible if you take the average to be the mean. But if you use the median it is quite possible. The diagram gives an example with seven boys and seven girls. Each light grey dot represents a male and each pink dot represents a female. A line connecting two dots indicates that they dated. The boy’s total is fourteen, for a mean of two. Obviously the girls must have the same total (since every line has two ends) so the girl's mean is also two. But the median is a different story. Sorting the boy's data gives us 0 1 1 3 3 3 3 for a median of 3 dating partners. After the girl's data is sorted we have 1 1 1 1 2 3 5 for a median of 1 dating partner. The medians do not necessarily have to be equal.

And of course there may have been a little bit of bragging on the part of the boys, and some coyness by the girls.