
Text
Unit C4 Section 3
Volumes of Pyramids, Cones and Spheres
The volumes of a pyramid, a cone and a sphere are found using the following formulae.
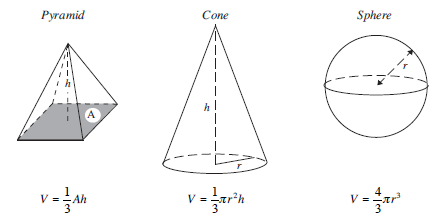
The proofs of these results are rather more complex and require mathematical analysis beyond the scope of this text.
Worked Examples
1
A cone and sphere have the same radius of 12 cm. Find the height of the cone if the cone and sphere have the same volume.

Suppose that the height of the cone is h cm.
| Volume of cone | = π × 122 × h = 48πh cm3 |
| Volume of sphere | = πr3 = π(12)3 = 2304π cm3 |
Since the volumes are equal
48πh = 2304π
Solving for h,
h = = = 48 cm

