Text
Unit F6 Section 5
Dealing With More Than One Inequality

If more than one inequality has to be satisfied, then the required region will have more than one boundary. The diagram below shows the inequalities x ≥ 1, y ≥ 1 and x + y ≤ 6 .

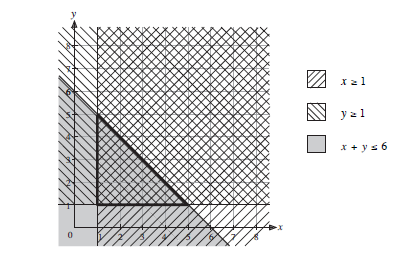
The triangle indicated by bold lines has all three shadings. The points inside this region, including those points on each of the boundaries, satisfy all three inequalities.

Worked Examples

1

Find the region which satisfies the inequalities

x ≤ 4,   y ≤ 2x,   y ≥ x + 1

Write down the coordinates of the vertices of this region.

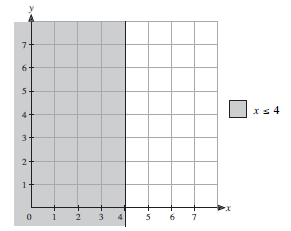
First shade the region which is satisfied by the inequality

x ≤ 4

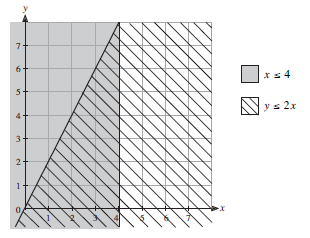
Then add the region which satisfies

y ≤ 2x

using a different type of shading, as shown.

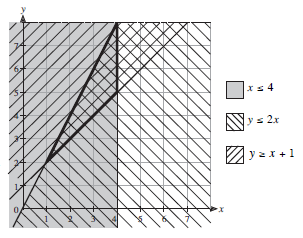
Finally, add the region which is satisfied by

y ≥ x + 1

using a third type of shading.

The region which has been shaded in all three different ways (the triangle outlined in bold) satisfies all three inequalities.

The coordinates of its vertices can be seen from the diagram as (1, 2), (4, 5) and (4, 8).

Note

When a large number of inequalities are involved, and therefore a greater amount of shading, the required region becomes more difficult to see on the graph.

Therefore it is better to shade out rather shade in, leaving the required region unshaded. This method is used in the following example, where 'shadow' shading indicates the side of the line which does not satisfy the relevant inequality. The region where all the inequalities are true is called the feasible region. All points inside the feasible region satisfy all the inequalities.

2

A small factory employs people at two rates of pay. The maximum number of people who can be employed is 10. More workers are employed on the lower rate than on the higher rate.

Describe this situation using inequalities, and draw a graph to show the feasible region in which they are satisfied.

Let x   =   number employed at the lower rate of pay,

and y   =   number employed at the higher rate of pay.

The maximum number of people who can be employed is 10, so x + y ≤ 10.

As more people are employed at the lower rate than the higher rate, then x > y.

As neither x nor y can be negative, then x ≥ 0 and y ≥ 0 .

These inequalities are represented on the graph below.

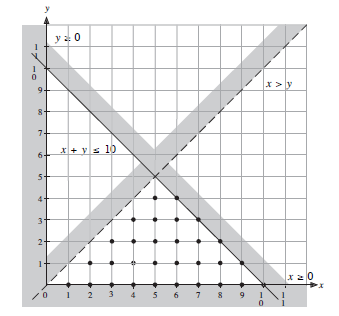
The triangle formed by the unshaded sides of each line is the region where all four inequalities are satisfied. The dots indicate all the possible employment options. Note that only integer values inside the region are possible solutions.

Note

Often there is a linear objective (e.g. profit or something similar) for which we need to find its optimal value (e.g. maximum or minimum), subject to a number of inequalities. This is called linear programming and it is an important topic.

We can solve linear programming problems easily by finding the value of the objective function at each vertex of the feasible region. The maximum and minimum values must occur at a vertex of the feasible region. We will illustrate this method in Worked Example 3, below.

3

The shaded area in the diagram below shows the solution of a set of inequalities in x and y. The variable x represents the number of boys in a cricket club and y represents the number of girls in the cricket club.

Use the graph above to answer the questions which follow.

(a)

State, using arguments based on the graph, whether the cricket club can have as members:

(i)

10 boys and 5 girls

No, as point (10, 5) is not in the feasible region.
(ii)

6 boys and 6 girls.

Yes, as point (6, 6) is in the feasible region.
(b)

Write down the set of THREE inequalities that define the shaded region.

y ≤ − + 12 ;   y ≥ 2 ;   y ≤ 2x
(c)

A company sells shirts for the club and makes a profit of £3.00 on a boy's shirt and £5.00 on a girl's shirt.

(i)

Write an expression in x and y that represents the total profit made by the company on the sale of shirts.

P = 3x + 5y
(ii)

Calculate the minimum profit the company can make.

The vertices are at (1, 2), ( 4, 8), (12, 2) and the corresponding values of P are £13 , £55 , £47 .

So the minimum profit is at (1, 2) of value £13.

Exercises

For each set of three inequalities, draw graphs to show the regions where all of the inequalities are satisfied. List the coordinates of the points which form the vertices of each region.

List the coordinates in the form: (0, 0), (1, 1)

(a)

x ≥ 2

y ≥ x + 1

y ≤ 3x

(b)

x ≥ 0

x ≤ 5

y ≥ x

(c)

x > − 2

y ≤ 2x + 3

y ≥ x − 2

(d)

x + y < 6

x > 2

y ≤ 3

(e)

y ≤ 2x + 1

y ≥ x − 1

x ≥ 2

(f)

y > x − 1

y > 2 − x

y ≥ 4

Each diagram shows a region which satisfies 3 inequalities. Find the three inequalities in each case.

(a)

x

y

y

(b)

x

y

y

(c)

x

y

y

(d)

x

y

y

(e)

x

y

y

(f)

y

y

y

A security firm employs people to work on foot patrol or to patrol areas in cars. Every night a maximum of 12 people are employed, with at least two people on foot patrol and one person patrolling in a car.

If x = the number of people on foot patrol

and y = the number of people patrolling in cars,

complete the inequalities below.

x + y ≤

x ≥

y ≥

Draw a graph to show the region which satisfies these inequalities.

In organising the sizes of classes, a head teacher decides that the number of students in each class must never be more than 30, that there must never be more than 20 boys in a class and that there must never be more than 22 girls in a class.

(a)

If x = the number of boys in a class

and y = the number of girls in a class,

complete the inequalities below.

x + y ≤

x ≤

y ≤

(b)

The values of x and y can never be negative. Write down two further inequalities.

Draw a diagram to show the region which satisfies all the inequalities above.

The diagram below shows a triangular region bounded by the lines y = x + 5,   y = −x + 5 and the line HK.

(a)

Write the equation of the line HK.

(b)

Write the set of three inequalities which define the shaded region GHK.

x

y

y

The school hall seats a maximum audience of 200 people for performances. Tickets for the Christmas concert cost £2 or £3 each. The school needs to raise at least £450 from this concert. It is decided that the number of £3 tickets must not be greater than twice the number of £2 tickets.

There are x tickets at £2 each and y tickets at £3 each.

(a)

Complete the inequalities to describe the situation above.

x + y 200

2x + 3y 450

y 2x

The graphs of   x + y = 200,   2x + 3y = 450   and   y = 2x   are drawn on the grid below.

(b)

Copy the grid and show by shading the region of the grid which satisfies all three inequalities in (a).

(i)

Hence find the number of £2 and £3 tickets which should be sold to obtain the maximum profit.

£2 and £3 tickets should be sold.
(ii)

State this profit.

£

At each performance of a school play, the number of people in the audience must satisfy the following conditions.

(i) The number of children must be less than 250.

(ii) The maximum size of the audience must be 300.

(iii) There must be at least twice as many children as adults in the audience.

On any one evening there are x children and y adults in the audience.

(a)

Write down the three inequalities which x and y must satisfy, other than x ≥ 0 and y ≥ 0 .

(i)

(ii)

(iii)

By drawing straight lines and shading on a suitable grid, indicate the region within which x and y must lie to satisfy all the inequalities.

Tickets for each performance cost £3 for a child and £4 for an adult.

(b)

Use your diagram to find the maximum possible income from ticket sales for one performance.

£

To make a profit, the income from ticket sales must be at least £600.

(c)

Use your diagram to find the least number of children's tickets which must be sold for a performance to make a profit.

tickets