Some relationships produce curves rather than straight lines when plotted.
Worked Examples
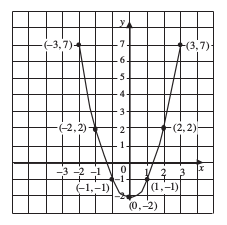
Complete the table below using the relationship y = x2 − 2.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y |

For each value of x the y value can be calculated using y = x2 − 2.
For example:
| If x = 3 then y | = 32 − 2 |
| = 9 − 2 | |
| = 7 |
| If x = 1 then y | = 12 − 2 |
| = 1 − 2 | |
| = −1 |
| If x = –2 then y | = (−2)2 − 2 |
| = 4 − 2 | |
| = 2 |
Calculating all the values gives the table.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y | 7 | 2 | –1 | –2 | –1 | 2 | 7 |
Write a list of coordinates using the data in the table.

The coordinates of the points to plot are (–3, 7), (–2, 2), (–1, –1), (0, –2), (1, –1), (2, 2) and (3, 7).
Plot the points and draw a smooth curve through them.

These points are plotted on the following graph and have been joined by a smooth curve.
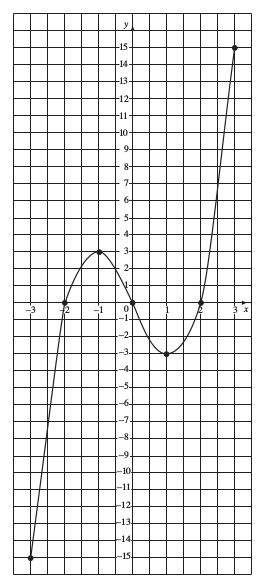
Draw the graph of y = x3 − 4x for values of x from –3 to 3.

The first step is to draw up and complete a table of values using the relationship
y = x3 − 4x, as below.
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y | –15 | 0 | 3 | 0 | –3 | 0 | 15 |
For example:
| If x = –3 then y | = (−3)3 − 4 × (−3) |
| = −27 + 12 | |
| = −15 |
| If x = 2 then y | = 23 − 4 × 2 |
| = 8 − 8 | |
| = 0 |
Each pair of values can be written as coordinates,
(–3, –15), (–2, 0), (–1, 3), (0, 0), (1, –3), (2, 0), (3, 15)
These can then be plotted and a smooth curve drawn through the points as shown in the following graph.