Text
Unit G3 Section 4
Tangents to Curves

A tangent is a line that touches a curve at one point only, as shown opposite.

The gradient of the tangent gives the gradient of the curve at that point. The gradient of the curve gives the rate at which a quantity is changing. For example, the gradient of a distance-time curve gives the rate of change of distance with respect to time, which gives the velocity.

Worked Examples

1

Draw the graph of y = x3 for −2 ≤ x ≤ 2. Draw tangents to the curve at x = –1 and x = 1. Find the gradients of these tangents.

The graph of y = x3 is shown below. The tangents have been drawn at x = –1 and x = 1.

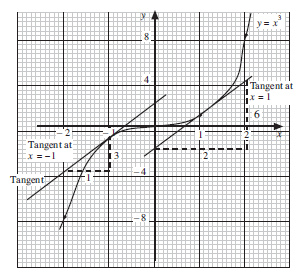
The triangles drawn under each tangent show that the gradients of both tangents are 3.
2

The height, h, of a ball thrown straight up in the air varies so that at time, t, h = 8t − 5t2 .

Plot a graph of h against t and use it to find:

(a) the speed of the ball when t = 0.6,

(b) the greatest speed of the ball.

The table below gives the values needed to plot the graph.

t(s) 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
h(m) 0 1.4 2.4 3.0 3.2 3.0 2.4 1.4 0

The graph is shown below.

(a) A tangent has been drawn at the point where t = 0.6. The gradient of this tangent is = 2. So the speed of the ball is 2 m/s.

(b) The speed of the ball is a maximum when the curve is steepest, that is at t = 0 and t = 1.6. At t = 1.6 the gradient is = −8. So the speed is 8 m/s.

The '–' sign indicates that the ball is moving down rather than up. You can say the ball moves down with speed 8 m/s or that the velocity of the ball is –8 m/s.
3

The following graph represents the cooling curve for a certain liquid.

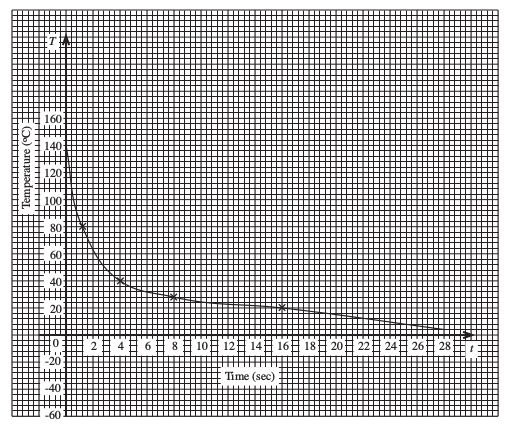
Use the graph to estimate

(a)

the temperature when the time, t, is 12 secs.

From the graph, temperature ≈ 24°C at time 12 secs.
(b)

the gradient of the curve when the time, t, is 4 secs.

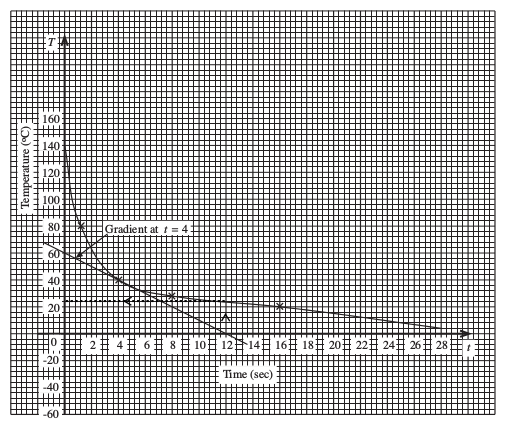
From the graph, gradient ≈ = 5 °C per sec.
4

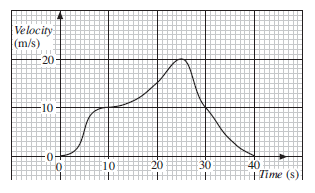
The graph shows how the velocity of a car changes.

Find:

(a) the time when the acceleration of the car is zero,

(b) the acceleration when t = 30.

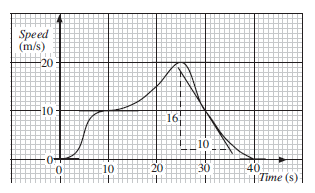
The acceleration of the car is given by the gradient of the velocity-time graph. There are 4 points where the gradient is zero, at t = 0, t = 10, t = 25 and t = 40. At each of these points a horizontal tangent can be drawn to the curve as shown opposite.

A tangent has been drawn to the curve at t = 30.

The gradient of this curve is = −1.6, so the acceleration is −1.6 m/s2.

Exercises

The height, h, of a ball at time, t, is given by, h = 10t − 5t2 .

The ball travels straight up and down.

Draw a graph of h against t for 0 ≤ t ≤ 2.

(a)

Use the graph to find the velocity of the ball when t = 0.5 and t = 1.2.

t = 0.5

t = 1.2

(b)

Find the maximum speed of the ball.

The graph below shows how the temperature of a can of drink increases after it has been taken out of a fridge.

Find the rate of change of temperature with respect to time, when;

(a)
t = 0, °C/min
(b)
t = 10, °C/min
(c)
t = 15. °C/min

Draw the graph of y = x3 for −3 ≤ x ≤ 3.

(a)

Find the gradient of the curve at x = –3, –2, –1, 0, 1, 2 and 3.

x–3–2–10123
gradient
(b)

Can you predict how to calculate the gradient of y = x3 for any value of x?

Gradient =

Draw a graph of y = sinx for 0 ≤ x ≤ 360°.

(a)

For what values of x is the gradient of the curve zero?

°, °
(b)

Find the maximum and minimum values of the gradient of the curve y = sinx , and state the values of x for which they are obtained.

maximum: at x = °

minimum: at x = °

Here is a velocity-time graph of a car travelling between two sets of traffic lights.

Calculate an estimate for the acceleration of the car when the time is equal to 20 seconds.

m/s2

The temperature, K, of a liquid t minutes after heating is given in the table below.

t
(time in minutes)		0102030405060
K
(Temp. in °C)		84614029272625

Using a scale of 2 cm to represent 10 minutes on the horizontal axis and a scale of 2 cm to represent 10 degrees on the vertical axis, construct a temperature-time graph to show how the liquid cools in the 60 minute interval.

Draw a smooth curve through all the plotted points.

Use your graph to estimate

(a)

the temperature of the liquid after 15 minutes

°C
(b)

the rate of cooling of the liquid at t = 30 minutes.

°C/min