Text
Unit J1 Section 2
Rotations

Rotations are obtained when a shape is rotated about a fixed point, called the centre of rotation, through a specified angle. The diagram shows a number of rotations.

It is often helpful to use tracing paper to find the position of a shape after a rotation.

Worked Examples

1

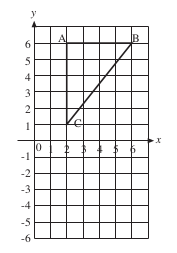
Rotate the triangle ABC shown in the diagram through 90° clockwise about the point with coordinates (0, 0).

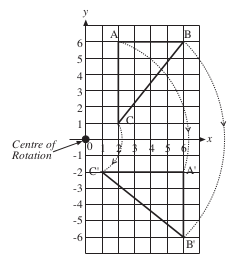
The diagram opposite shows how each vertex can be rotated through 90° to give the position of the new triangle.
2

The diagram shows the position of a shape A and the shapes, B, C, D, E and F which are obtained from A by rotation.

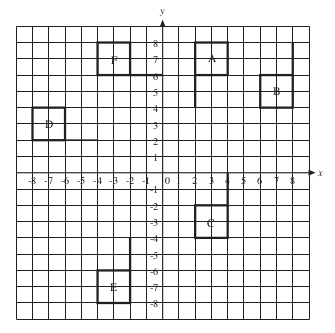
Describe the rotation which moves A onto each other shape.

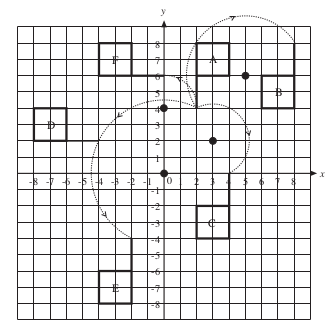
Each rotation is now described.

•   A to B: Rotation of 180° about the point (5, 6).
•   A to C: Rotation of 180° about the point (3, 2).
•   A to D: Rotation of 90° anti-clockwise about the point (0, 0).
•   A to E: Rotation of 180° about the point (0, 0).
•   A to F: Rotation of 90° anti-clockwise about the point (0, 4).

Exercises

The diagram shows the position of a shape labelled A and other shapes which were obtained by rotating A.

(a)

Describe how each shape can be obtained from A by a rotation.

A to B: , centre (, )

A to C: , centre (, )

A to D: , centre (, )

A to E: , centre (, )

(b)

Which shapes can be obtained by rotating the shape E?

A
B
C
D

The shape A has been rotated to give each of the other shapes shown. For each shape, find the centre of rotation.

(a)
A → B (, )
(b)
A → C (, )
(c)
A → D (, )
(d)
A → E (, )
(a)

Describe how each shape shown below can be obtained from A by a rotation.

A to B: , centre (, )

A to C: , centre (, )

A to D: , centre (, )

A to E: , centre (, )

(b)

Which shapes cannot be obtained from C by a rotation?

A
B
D
E

The shape B can be obtained from A by two rotations. Describe these rotations.

, centre (, ),

followed by

, centre (, )